Neural Decoding With Kernel-Based Metric Learning

Overview

Given a sample of data points, we often assume the points reside in some space in which we can measure distances between pairs of points. From these measurements we can understand which points are close to each other. Nearby points are often assumed to share characteristics. This assumption is the foundation of nearest-neighbor classification and regression as well as clustering.

The function that measures the distance between pairs of points in a particular space is called a distance metric.

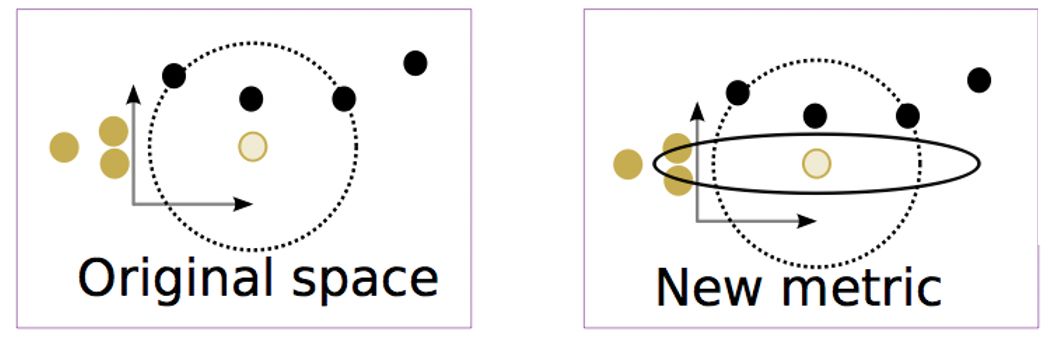
When studying the function of the nervous system, the choice of metric for the neural responses is a pivotal assumption. A well-suited distance metric enables neuroscientists to gauge the similarity of neural responses to various stimuli and assess the variability of responses to a repeated stimulus. In particular, neural spike train metrics have been used to quantify the information content carried by the timing of action potentials. While a number of metrics for individual neurons exist, a method to optimally combine single-neuron metrics into multi-neuron, or population-based, metrics is lacking. For time-locked neural responses, we pose the problem of the supervised optimization of multi-neuron metrics and other metrics (including those for local field potentials (LFPs), which are the electric potentials measured within brain tissue). The goal is to tune the metric to better predict the stimulus from the neural response. Predicting the stimulus from the response is known as neural decoding.

To guide the choice of metric learning, we propose to use centered alignment, a kernel-based dependence measure, to measure the correlation between the similarity in the data space (determined by the metric) and the similarity in the stimulus space. We provide mathematical formulation of the appropriate kernel and distance functions, as well as a MATLAB implementation of the batch and mini-batch optimization of the centered alignment metric learning (CAML).