Quantifying the Informativeness of Similarity Measurements

Overview

Choosing the particulars of a data representation is crucial for the successful application of machine learning techniques. In the unsupervised case, there is a lack of measures that can be used to compare different parameter choices that affect the representation. In this paper, we describe an unsupervised measure for quantifying the ‘informativeness’ of correlation matrices formed from the pairwise similarities or relationships among data instances.

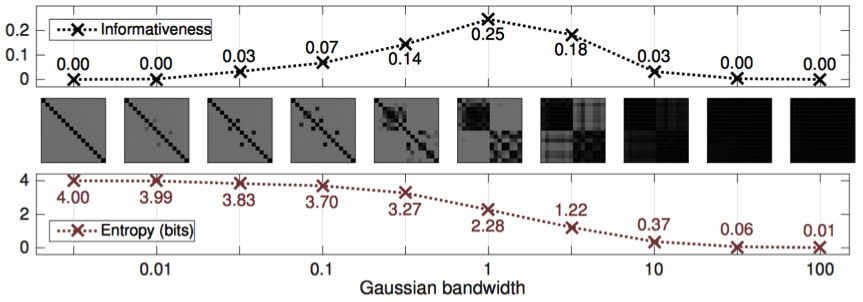
The measure quantifies the heterogeneity of the correlations and is defined as the distance between a correlation matrix and the nearest correlation matrix with constant off-diagonal entries. While a homogenous correlation matrix indicates every instance is the same or equally dissimilar, informative correlation matrices are not uniform, some subsets of instances are more similar and themselves are dissimilar to other subsets. A set of distinct clusters is highly informative (Figure 1).

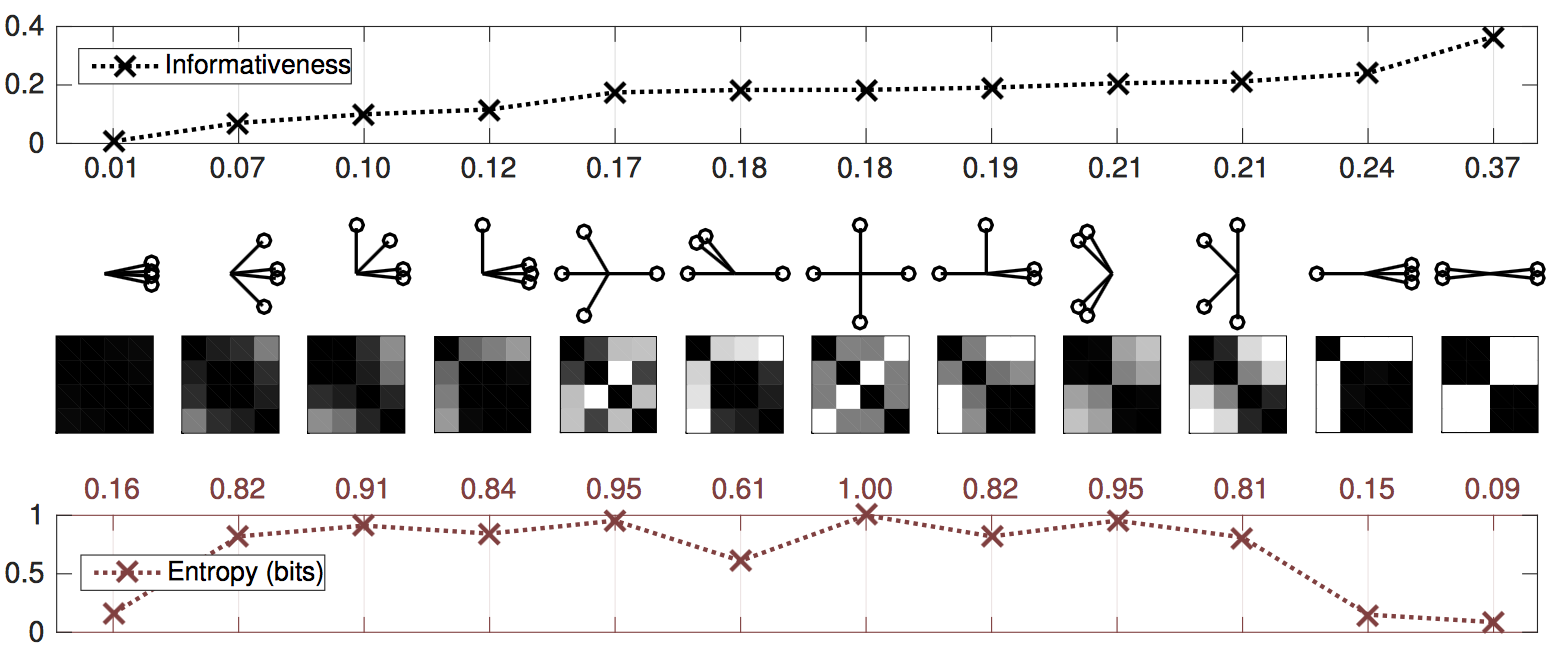
Informativeness can be used as an function to choose between representations or perform parameter selection (Figure 2) or dimensionality reduction. Using it, we designed a convex optimization algorithm for de-noising correlation matrices that clarifies their cluster structure.