Timekeeping in the Interplanetary Internet

Briefing Slides

Interplanetary Timekeeping PostScript | PowerPoint | PDF

Importance of the Problem

There is a long tradition in the planetary science community of controlling experiments entirely from Earth, although there is some progress using semi-autonomous vehicles for Mars surface exploration. Most missions require some kind of clock to determine windows of communication opportunities, for example. During periods where communication with Earth is not possible, there is need to synchronize clocks among the orbiters, rovers and landers participating in the mission.

The Interplanetary Internet (IPIN) consists of stations in the vicinity of Earth and stations in the vicinity of Mars, as well as the radio and/or optical space links between them. This project explores synchronization issues in the IPIN using suitable modifications to the Network Time Protocol (NTP) and the Consulting Committee on Space Data Systems (CCSDS) Proximity-1 Space Link Protocol. NTP is widely used to synchronize computers in the Earth Internet and has been deployed in low-orbit Earth orbiters, but not in interplanetary missions. Proximity-1 is now used for space data links between vehicles on and near Mars. There are three issues which distinguish the Earth Internet from the IPIN: bodies are moving, connectivity between them is necessarily not continuous and transmission delays can be very long.

Brief Description of Work and Results

With support from Jet Propulsion Laboratories (JPL) and NASA, we are studying timekeeping issues in the IPIN, specifically for Mars missions and supporting infrastructure. Currently, the clocks for all space vehicles are coordinated from Earth using the facilities of the Deep Space Network (DSN) operated by JPL. With new technology timekeeping in space would be distributed so that timed experiments could be accurately controlled autonomously and without intervention from Earth.

There are three issues which distance the new technology from current NTP practice: bodies are moving in an inertial frame, connectivity between them is necessarily not continuous and transmission delays can be very long.

The IPIN would includes three segments. The Earth segment consists of the current Internet, including science experiment hosts, various Earth stations and satellites, and the Moon. The DSN segment includes the DSN stations in California, Spain and Australia, as well as the various space vehicles orbiting the planets and the Sun. . The Mars segment includes the various orbiters, landers and rovers in the vicinity of Mars.

While the current NTP technology is applicable in the Earth segment and the Mars segment and could in principle be adapted for the DSN segment, there are practical difficulties when using the traditional Internet model. Satellite communications and navigation functions require extremely precise range and range rate (Doppler) measurements which require and transceiver support which NTP in its present form is unable to utilize.

The mission of this project is to develop an understanding of the timekeeping issues in the IPIN, including the effects of orbit mechanics, general relativity and intermittent connectivity. The work will explore scenarios where NTP timestamps can be embedded in the Proximity-1 protocol and how NTP functionality can be provided in space networks in the vicinity of Earth and Mars.

The goals of the project are to

• Explore means to establish a uniform timescale onboard spacecraft while retaining a UTC spacecraft clock (SCLK). This enables spacecraft to discipline other spacecraft in time and frequency.
• Enhance the Proximity-1 protocol to encode and transmit NTP timestamps.
• Develop a model where Mars spacecraft can determined crosstrack passes and exchange navigation, communication and time transfer functions.
• Demonstrate a proof-of-concept model in the form of a space network simulator using components from the JPL SPICE toolkit.

Approach

We have developed an analysis of the important issues with time transfer in space, including orbit mechanics, general relativity, spacecraft technology now in common use. We have proposed modifications to the Proximity-1 protocol that supports NTP timestamps. We have developed a space network simulator and used it to model a candidate scenario involving five Earth satellites in various orbits together with one lander.

We are studying possible scenarios to deploy this technology in the vicinity of Earth and in the vicinity of Mars.

 

Our model is that the timescales for all platforms, be they in space or on the surface, are coordinated with proper time on Earth, which is called TT. It runs at the same rate as atomic time (TAI), but at a fixed offset from it. However, the timescales on other objects in a barycentric from do not run at this rate due to the effects of general relativity, specifically gravitational redshit and time dilation. We assume all timescales in use have been corrdinated at a given time and that the time offset at any other time is computable given the known motion of the object.

 

The lightwave propagation time between two moving objects in space can be determined by an iterative procedure. Let P_s(t) be the position of the server at barycentric time (TDB) t according to the server ephemeris and P_c(t) be the position of the client at time t according to the client ephemeris. The propagation time T_p between the server and client (called lighttime in SPICE) is the unique number that satisfies

      | Pc(Ts + Tp) - Ps(Ts) |
Tp =  -----------------------,
                c
    

where the quantity in brackets is the distance between the server and client at the times specified and c is the speed of light. The following iterative procedure is adapted from SPICE, and the description is adapted from the SPICE documentation.

Time can be disciplined on a one-way or two-way basis. In a one-way scheme a server with a presumed correct clock broadcasts a packet including the TDB time T_s and ephemeris position P_s(t) at time t = T_s. When the packet arrives, the client determines an ephemeris position P_c(t) at time t = T_s + T_p(0), where T_p(0) = 0 is an initial estimate. At each new iteration i, the client finds a new position P_c(t) at time t = T_s + T_p(i- 1). The algorithm can be concisely expressed

Tp(0) = 0;

        | Pc(Ts + Tp(i - 1)) - Ps(Ts) |
Tp(i) = ------------------------------  (i > 0).
                       c
    

The SPICE documents state that the sequence T_p(0), T_p(1), ... converges geometrically. Moreover, it can be shown that the difference between T_p and T_p(i) satisfies the following inequality.

| Tp - Tp(i) | < Tp * (V / c)i+1,
    

where V is the speed of the client with respect to the solar system barycenter and c is the speed of light. For nearly all objects in the solar system V is less than 60 km/s, so after only one iteration the relative error | T_p - T_p(i) | is not more than 20 microseconds per astronomical unit (AU) of distance between server and client. For objects within the solar system, the error is less than 1 ms, which is within the error expectations for NTP timekeeping in the Interplanetary Internet. The difference between the final time estimate T_s + T_p(1) and the local clock is the offset presented to the NTP filtering and discipline algorithms, which function in the normal way.

A two-way scheme is similar to the NTP symmetric mode involving two peers. Each peer sends a packet at intervals to be determined. The packet contains the same information as in the one-way scheme and in addition the originate and receive timestamps as in NTP symmetric mode. In addition, the barycentric coordinates for each of the three timestamps is convened in extension fields. The advantage of this scheme is the same as for NTP symmetric mode. Each peer can independently measure the TDB offset of the other as well as the overall roundtrip delay.

We anticipate a network of NTP peers where each platform is in intermittent contact with one or more other peers and where the NTP subnet is continuously evolving and reconfiguring according to a fixed or ad hoc schedule. Existing features of NTP, especially the Manycast autoconfiguration mode are directly applicable, as well as the Autokey authentication scheme.

It may will happen that residual clock frequency offsets may introduce considerable error if the time between updates is relatively long, as would be expected during communication opportunities between Earth and mission spacecraft. After a few measurements the frequency can be disciplined in the usual way, but this affects the position and velocity vectors and residuals with respect to the ephemeris. What makes frequency-induced errors more nasty is that the frequency may fluctuate due to spacecraft thermal cycles and power management. Assuming primary servers on Earth together with ephemerides of the transmitter location, the above scheme continues to refine the residuals and develop global time. Kalman filters or ARIMA methods might be a good tool to deal with the residuals and steer to the best time.

Current Status in 2005

Harish Nair has searched the JPL SPICE library and documentation for means to predict position and velocity vectors for moving objects in space and on planetary surfaces. He has used the available algorithms and ephemerides to convert TDB time to entity position, which is the basis for the time transfer technique described above. We have found example data for the Earth, Moon, other planets and an interplanetary mission. While these data are highly useful in initial testing and evaluation, we will eventually need additional interesting scenarios involving Mars orbiters and surface platforms.

We have adapted the NTP software distribution to function both as a daemon for ordinary time synchronization means and also as a simulator for space operations. This capability has been integrated in the public release for others to experiment with. The adaptations include replacing the routines to read and set the clock, some routines of the I/O system and the main program, which implements the simulator queue and utility routines. Whether the daemon or simulator function is enabled is selected in the software configuration process. A description and status report is on the NTP Discrete Event Simulator page

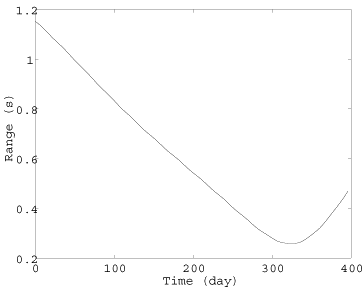
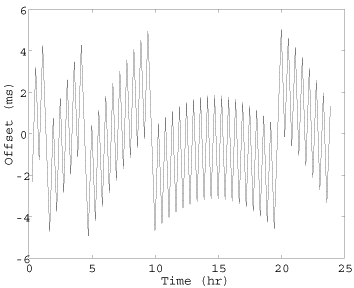
The graphs above show the results of these experiments. The graph on the left shows the light time between the Moon and Mars calculated from the ephemerides over more than a year. Clearly, the range narrows from over a second to aboutt 270 milliseconds and then widens again. The graph on the right shows the fine structure of the offset computed by NTP after light time correction. The residual errors appear as complex wiggles with amplitude a few milliseconds. Very likely these are due to residuals incident to the polynomial approximation used in the ephemeris calculation. This might not surprise hardened space hands, but it sure surprised the simulator. However, all this means is that the clock discipline tuning parameters for near-Earth baselines might be quite different for interplanetary baselines and the accuracy and precisions achievable might not be nearly as good.

Future Plans

The general plan is to evaluate the above approach in detail, especially the impact of ephemerides jitter and oscillator wander. We can simulate the effects of oscillator wander, but the effects of ephemerides jitter will need to be explored in more detail. Our immediate plans are to run experiments with different clock discipline tuning parameters.