we model image noise as
white, zero-mean Gaussian noise, with a standard
deviation σ, and assume the noisy image I can be
decomposed into a latent image
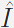 and noise η: and noise η: |
|
|
 |
(1) |
| where x is the pixel
index. |
|
Multi-view Block Matching |
| we
present a multi-view block matching (MVBM)
technique for patch-based image denoising. The
goal of MVBM is to find similar patches from
HR-M image pairs for each patch in HS-M (or
HR-C) images. |
|
Patch-Based Denoising |
|
Based on the image noise formulation Eq.(1), we design
a new full-spectrum spatial regularization that
uses patches from the HR-M images to add back
the high frequency details for HS-M images. We
formulate the full-spectrum denoising as: |
|
|
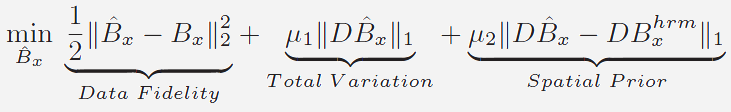 |
(2) |
where 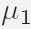 and and
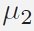 are two positive weights
used to control the strength of TV and spatial
prior regularization respectively; || · ||1
represents the ℓ1-norm. are two positive weights
used to control the strength of TV and spatial
prior regularization respectively; || · ||1
represents the ℓ1-norm.
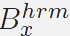 is obtained from our MVBM method. We choose
ℓ2-norm for the data fidelity term since noise
is obtained from our MVBM method. We choose
ℓ2-norm for the data fidelity term since noise
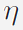 is assumed to be additive and Gaussian. We also
add a Total Variation(TV) regularization term to
the data fidelity term to make the
reconstruction process more reliable.
is assumed to be additive and Gaussian. We also
add a Total Variation(TV) regularization term to
the data fidelity term to make the
reconstruction process more reliable. |
|
Iterative Optimization |
Compared with Tikhonov-like regularization, the
minimization problem formulated by Eq.(2) is
computationally expensive to solve due to
nonlinearity and non-differentiability of the
regularization terms. we present an effective
solution: we introduce two auxiliary vectors u,
v ∈
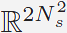 to the objective function in Eq.(2)
and then reformulate this denoising problem
equivalently as an optimization problem with
linear constraints to the objective function in Eq.(2)
and then reformulate this denoising problem
equivalently as an optimization problem with
linear constraints |
|
|
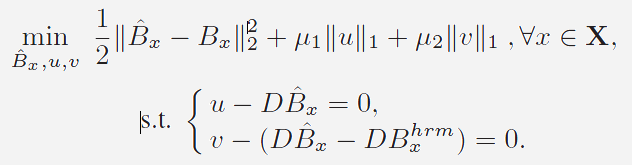 |
(3) |
|
To solve for the Eq.(3), we apply the
alternating minimization method to the augmented
Lagrangian function of Eq.(3) using the
following iterative scheme: |
|
|
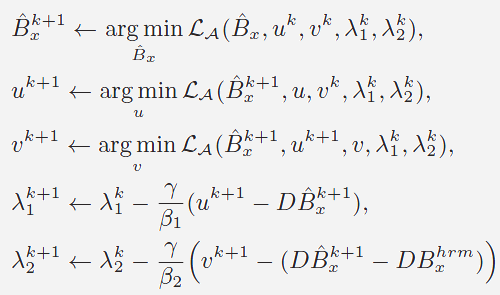 |
(4a)
(4b)
(4c)
(4d)
(4e) |
where
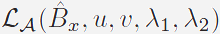 is the augmented Lagrangian function of
Eq.(3) defined by is the augmented Lagrangian function of
Eq.(3) defined by |
|
|
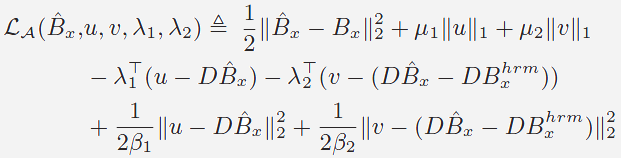 |
(5) |
where
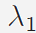 and and
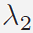 are two vectors of Lagrange
multipliers and are two vectors of Lagrange
multipliers and
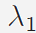 , ,
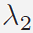 ∈ ∈
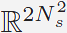 , ,
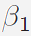 and and
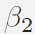 are
penalty parameters and γ is the step length for
updating are
penalty parameters and γ is the step length for
updating
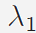 and and
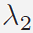 . By iteratively updating the
Lagrange multipliers . By iteratively updating the
Lagrange multipliers
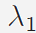 and and
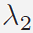 , the solution to
Eq.(4a)-(4e) will eventually converge to the one
to Eq.(3). , the solution to
Eq.(4a)-(4e) will eventually converge to the one
to Eq.(3). |
|
|
|
|














