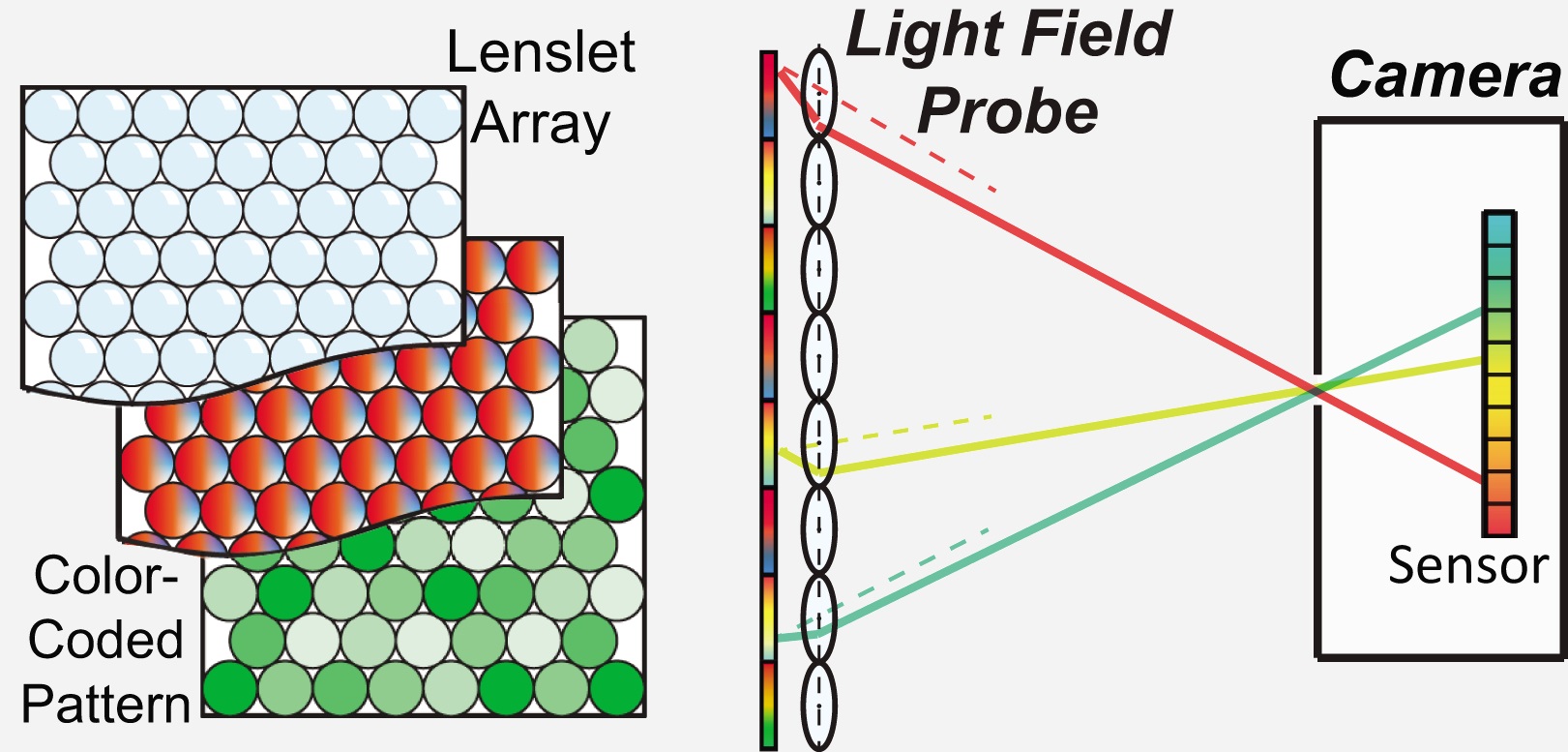
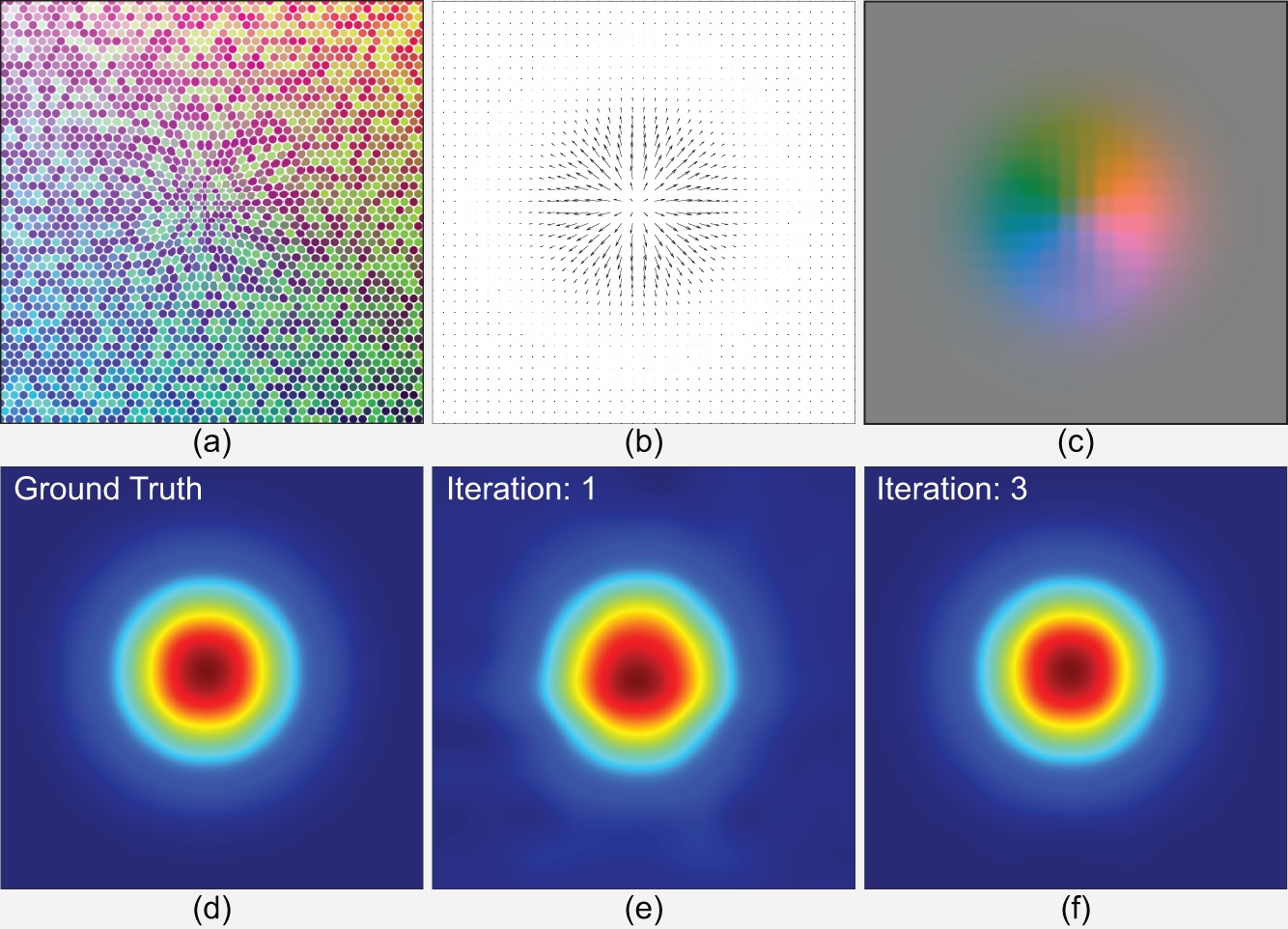
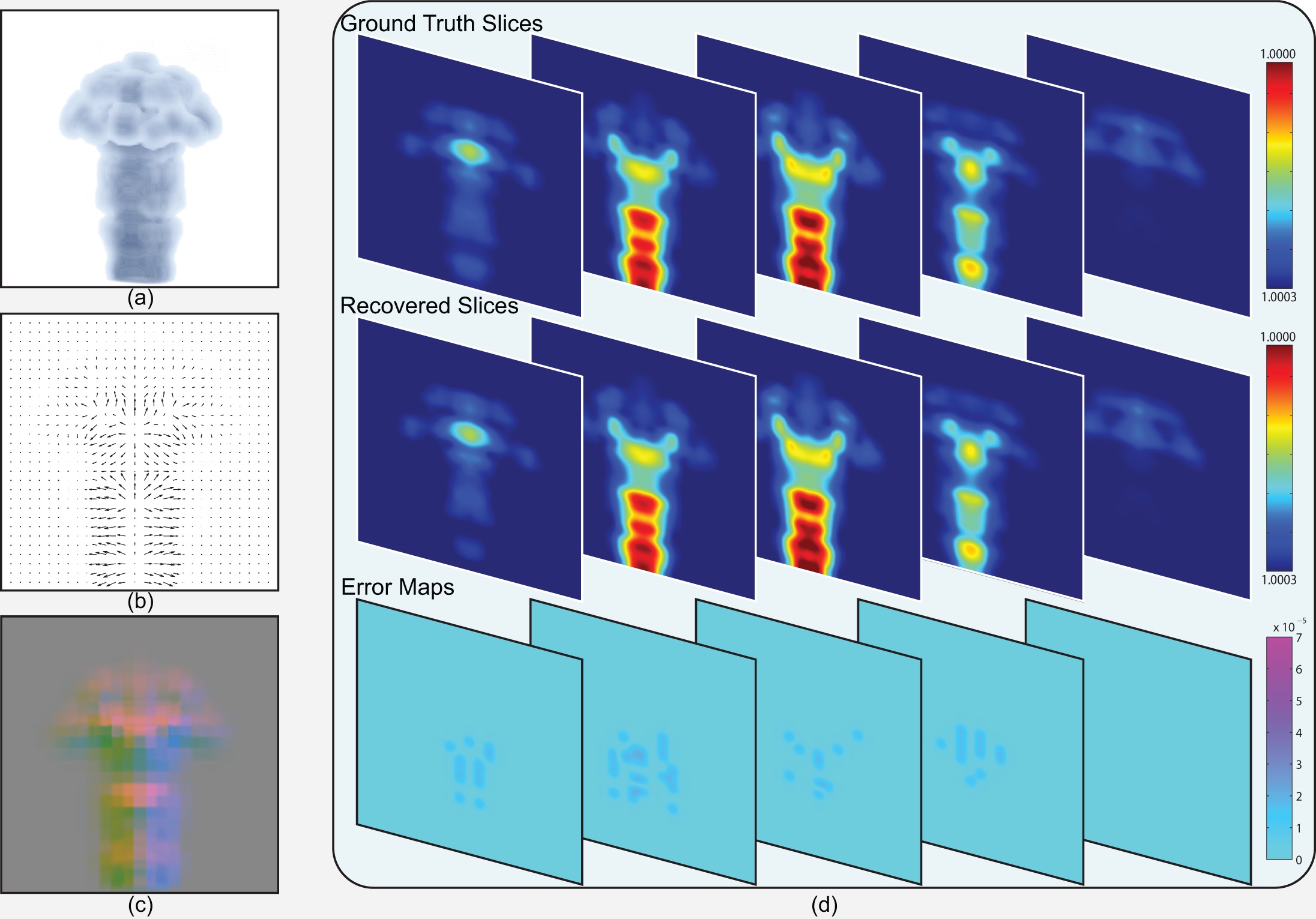
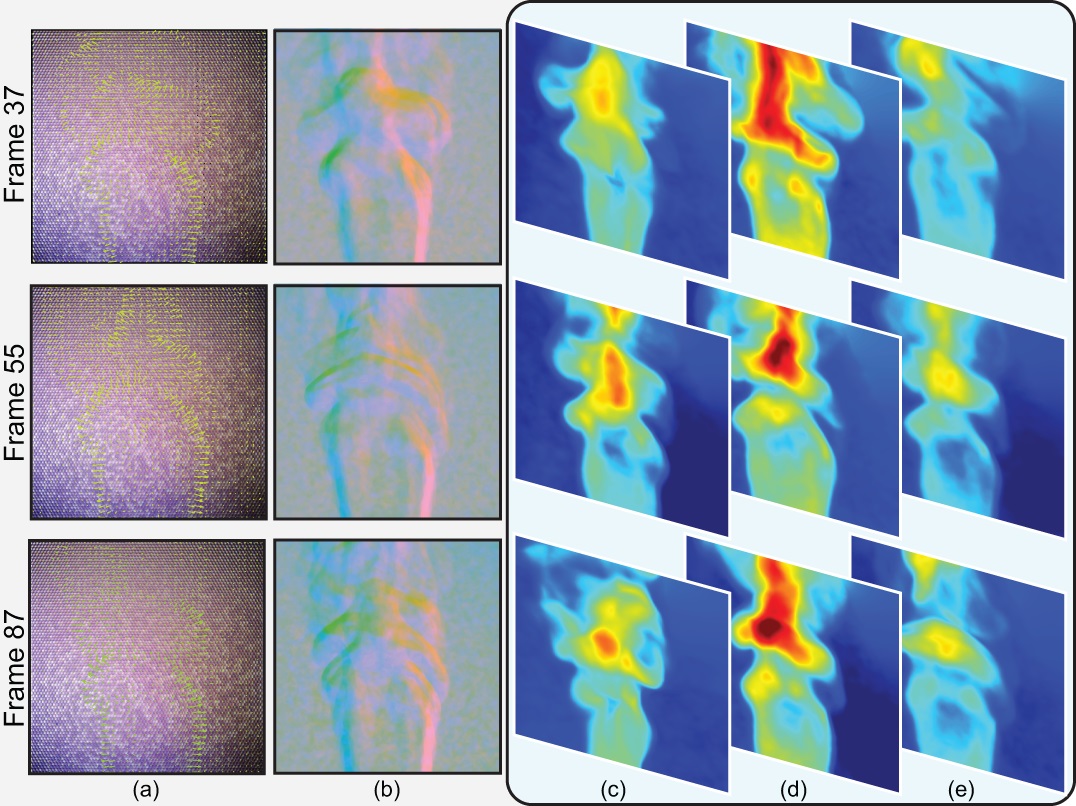
| Transparent gas flows are difficult to reconstruct: the refractive index field (RIF) within the gas volume is uneven and rapidly evolving, and correspondence matching under distortions is challenging. We present a novel computational imaging solution by exploiting the light field probe (LFProbe). A LF-probe resembles a view-dependent pattern where each pixel on the pattern maps to a unique ray. By observing the LF-probe through the gas flow, we acquire a dense set of ray-ray correspondences and then reconstruct their light paths. To recover the RIF, we use Fermat’s Principle to correlate each light path with the RIF via a Partial Differential Equation (PDE). We then develop an iterative optimization scheme to solve for all light-path PDEs in conjunction. Specifically, we initialize the light paths by fitting Hermite splines to ray-ray correspondences, discretize their PDEs onto voxels, and solve a large, over-determined PDE system for the RIF. The RIF can then be used to refine the light paths. Finally, we alternate the RIF and light-path estimations to improve the reconstruction. Experiments on synthetic and real data show that our approach can reliably reconstruct small to medium scale gas flows. In particular, when the flow is acquired by a small number of cameras, the use of ray-ray correspondences can greatly improve the reconstruction. |
LF Probe-based Acquisition System
|