Computational Results for the Minimum Vertex Separator Problem
[MLBP] WILLIAM W. HAGER, JAMES T. HUNGERFORD, AND ILYA SAFRO "A MULTILEVEL BILINEAR PROGRAMMING ALGORITHM FOR THE VERTEX SEPARATOR PROBLEM", 2014
Download graphs
The Vertex Separator Problem for a graph is to find the smallest collection of vertices whose removal breaks the graph into two disconnected subsets that satisfy specified size constraints.
Let G = (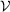 ,
,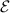 ) be a graph on vertex set
) be a graph on vertex set 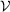 = {1,2,…,n} and edge set
= {1,2,…,n} and edge set 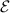 ⊂
⊂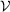 ×
×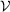 .
We assume G is simple and undirected; that is for any vertices i and j we have
(i,i)
.
We assume G is simple and undirected; that is for any vertices i and j we have
(i,i)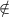
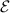 and (i,j) ∈
and (i,j) ∈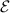 if and only if (j,i) ∈
if and only if (j,i) ∈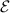 (note that this implies that |
(note that this implies that |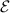 |, the
number of elements in
|, the
number of elements in 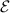 , is twice the total number of edges in G). For each i ∈
, is twice the total number of edges in G). For each i ∈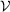 ,
let ci denote the cost and wi > 0 denote the weight of vertex i. If
,
let ci denote the cost and wi > 0 denote the weight of vertex i. If 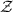 ⊂
⊂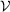 ,
then
,
then
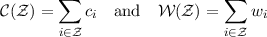
denote the total cost and weight of the vertices in 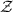 , respectively.
, respectively.
If the vertices 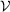 are partitioned into three disjoint sets
are partitioned into three disjoint sets 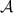 ,
, 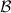 , and
, and 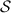 , then
, then 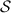 separates
separates 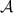 and
and 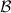 if there is no edge (i,j) ∈
if there is no edge (i,j) ∈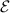 with i ∈
with i ∈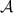 and j ∈
and j ∈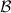 . The Vertex
Separator Problem (VSP) is to minimize the cost of
. The Vertex
Separator Problem (VSP) is to minimize the cost of 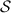 while requiring that
while requiring that 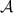 and
and 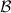 have approximately the same weight. We formally state the VSP as follows:
have approximately the same weight. We formally state the VSP as follows:
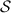 =
= 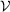 \ (
\ (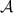 ∪
∪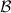 ) and
) and 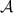 ∩
∩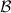 = ∅ ensure that
= ∅ ensure that 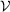 is partitioned into disjoint
sets
is partitioned into disjoint
sets 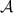 ,
, 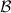 , and
, and 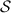 , while the constraint (
, while the constraint (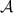 ×
×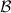 ) ∩
) ∩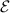 = ∅ ensures that there are
no edges between the sets
= ∅ ensures that there are
no edges between the sets 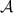 and
and 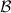 .
.
| Graph | Best known VSP [MLBP] |
| bcspwr09 | 7 |
| bcsstk17 | 198 |
| c-38 | 14 |
| c-43 | 84 |
| ca-HepPh | 677 |
| crystm01 | 65 |
| delaunay_n13 | 68 |
| email-Enron | 690 |
| email-EuAll | 10 |
| Erdos992 | 88 |
| fxm3_6 | 47 |
| G42 | 472 |
| jagmesh7 | 14 |
| lshp3466 | 57 |
| minnesota | 17 |
| nasa4704 | 172 |
| net25 | 510 |
| netscience | 0 |
| netz4504 | 17 |
| oregon2_010505 | 59 |
| p2p-Gnutella04 | 2062 |
| p2p-Gnutella05 | 1642 |
| p2p-Gnutella06 | 1375 |
| p2p-Gnutella08 | 959 |
| p2p-Gnutella09 | 1211 |
| p2p-Gnutella24 | 3062 |
| p2p-Gnutella25 | 2543 |
| p2p-Gnutella30 | 3860 |
| p2p-Gnutella31 | 5873 |
| sherman1 | 28 |
| soc-Epinions1 | 3061 |
| sstmodel | 22 |
| USpowerGrid | 8 |
| barth5_1Ksep_50in_5Kout | 987 |
| bcsstk30_500sep_10in_1Kout | 376 |
| befref_fxm_2_4_air02 | 932 |
| bump2_e18_aa01_model1_crew1 | 5988 |
| c-30_data_data | 464 |
| c-60_data_cti_cs4 | 2795 |
| data_and_seymourl | 1137 |
| finan512_scagr7-2c_rlfddd | 5921 |
| mod2_pgp2_slptsk | 7934 |
| model1_crew1_cr42_south31 | 2059 |
| msc10848_300sep_100in_1Kout | 279 |
| p0291_seymourl_iiasa | 970 |
| sctap1-2b_and_seymourl | 4010 |
| south31_slptsk | 2327 |
| vibrobox_scagr7-2c_rlfddd | 2821 |
| web-NotreDame | 272 |
| web-Stanford | 124 |
| wiki-Vote | 762 |
| yeast | 180 |