Program #2

Due April 17

This is a combination HW and programming assignment. We will be using a very robust, fast, and efficient datalog implementation called DLV to practice with knowledge representation and reasoning. For many people, representing knowledge in a form that can be used by a computer for automated reasoning, although really just another form of computer programming, can seem rather difficult (much in the same way that students happy to write 500 lines of C code fall apart at a 3-line Lisp/Scheme recursion :-) That is, if all you have is a hammer, every problem looks like a nail. (Worse, to carry the analogy way past the breaking point, a bad Lisp programmer can force Lisp into just another hammer mode, but there's almost no way to do that with pure logic :-) In any case, there are other ways to conceptualize the act of programming besides "imperative" (C/Java/Pascal/Fortran-like), and "Logic Programming" is one of them. The upshot: START EARLY OR YOU WILL NOT FINISH THE ASSIGNMENT.

DLV is available for Solaris, Linux, FreeBSD, MacOS, and Windows at http://www.dbai.tuwien.ac.at/proj/dlv/. Also available there is a simple manual, and a link to a nice tutorial. For the problems that use DLV, you need to hand in a complete listing of your program, including the intended interpretation for all symbols used and a trace of the DLV session to show it runs. You can just use plain disjunctive datalog.

1. [12 points] Getting Acquainted. Consider the following axioms:

• Horses are faster than dogs
• There is a greyhound that is faster than every rabbit
• Harry is a horse
• Ralph is a rabbit

We would like to prove Harry is faster than Ralph

1a. Write each sentence in FOPC.

1b. Write any additional assumptions that you need (world knowledge) in FOPC.

1c. Convert each sentence into CNF.

1d. Convert each sentence (or your CNF) into Datalog format.

1e. By hand, do a resolution proof that Harry is faster than Ralph. (show your work)

1d. Use DLV to prove the same thing.

2. [13 points] A man and  a woman are forced to share a table in a coffeehouse. They're dressed alike and take an instant dislike to each other. The one with brown eyes says "I'm a man." The one with blue eyes says, "I'm a woman." At least one is lying. Who is who?

3. [25 points] Model-based diagnosis. Consider the domain of house plumbing represented in the following diagram:

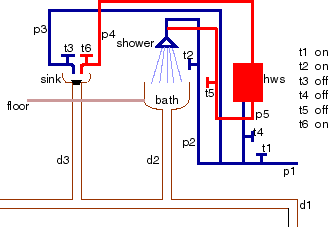
The Plumbing Domain  

In this example constants p1, p2 and p3 denote cold water pipes. Constants t1 through t6 denote taps and d1, d2 and d3 denote drainage pipes. The constant shower denotes a shower, bath denotes a bath, sink denotes a sink and floor denotes the floor. The diagram above is intended to give the denotation for the symbols.

Suppose we have as predicate symbols:

• pressurized , where pressurized(P) is true if pipe P has mains pressure in it.
• on , where on(T) is true if tap T is on.
• off , where off(T) is true if tap T is off.
• wet , where wet(B) is true if B is wet.
• flow , where flow(P) is true if water is flowing through P.
• plugged , where plugged(S) is true if S is either a sink or a bath and has the plug in.
• unplugged , where unplugged(S) is true if S is either a sink or a bath and has the plug out.

The file plumbing.dlv contains a Datalog axiomatization for this domain.

2a. [5 pts] Unfortunately there is a bug in the program. We know this because we can prove that the floor is wet, even though it isn't wet in the intended interpretation. Which clause is incorrect? How should it be fixed?

2b. [20 pts] Using your fixed axiomatization, remove the assertions about t1 and t4 (let's assume they are down in the basement where they cannot be observed). Using the remaining observations about the taps and that the sink is plugged, extend the theory to allow you to deduce the state of t1 and t4 given that you observe that the floor is wet and the sink is wet. (for example, in the theory we have given you, deleting the facts about t1 and t4 and adding wet(floor) and wet(sink) will result in a single model that does not say anything about the state of t1 and t4).

Do this without using DLV's negation primitives, so represent that taps for example can be either on or off, and use both disjunctive assertions (i.e. taps are either on or off) and integrity constraints (i.e. a tap cannot be both on and off at the same time).

4. [20 points] Use DLV to solve problem 1 on HW#3 (first name, last name, job, dinner). Hint: the tutorial shows one way to do this (as does the amb interpreter discussed in the undergraduate 280 Scheme class)

5. [30 points, 6 each] Consider a geographical database (here). The database has the schema listed below.

       state(name,abbreviation,captial,population,area,orderJoinedUSA,
                largestcity,secondlargest,third,fourth)

city(state,stateabbrev,name,population)

       river(riverName, length)
       riverin(riverName,state).

borders(state,state).
highlow(state, abreviation, highPlace, height1, lowPlace, height2)
mountain(state, abreviation, mountainName, height)
lake(lakeName, size)
lakein(lakeName,state).

        road(roadName,state).

Formulate the following queries in Datalog.

UNDERGRADUATES (481):

5a.What are the names of states that border Delaware?

5b. What roads travel through Delaware and the adjacent states?

5c. Which rivers run through at least five different states?

5d. Which single road should I take to get from from Delware to New York?

5e. What states border on states through which the Rio Grande runs?

GRADUATES (681): Either answer the questions, or explain why they cannot be answered. You may need to use some of the more advanced features such as negation.

5a. What is the most populous state?

5b. What rivers flow through states that border the state with the largest
       population?

5c. What is the largest state through which the Mississippi runs?

5d. What is the length of the river that runs through the most states?

5e. Find a connected route from the state containing Philadelphia to the state containing Los Angeles.