|
Written
Homework #5
Due
May 3
1. [30 points] Planning Graph
Construction
Shakey, the overworked robot,
is faced with a planning problem. The task he must perform is to move
n boxes from room A to room B. He can only perform two actions, MoveBoxA2B
and MoveB2A. In MoveBoxA2B, Shakey moves himself and a box from A to
B. In MoveB2A, Shakey moves from B to A, without moving any boxes. The
world will be represented as follows:
- Constants: box1, box2,..., boxn, Shakey, A (room A), and B (room
B)
- Predicates: At(object, location)
- Actions:
MoveBoxA2B(boxi)
PRECOND: At(boxi,A), At(Shakey,A)
ADD: At(boxi,B), At(Shakey,B)
DELETE: At(boxi,A), At(Shakey, A)
MoveB2A()
PRECOND: At(Shakey,B)
ADD: At(Shakey,A)
DELETE: At(Shakey, B)
(a) [5 points] For the moment, assume that we have only the two boxes
box1 and box2,both
in room A, and that Shakey also starts out in room A. Write down the
first three levels of the planning graph for this problem, i.e., S0,
A1, and S1. Show all propositions and all edges, include the maintainance/persistence
actions. Write all mutex constraints underneath each level in the
graph (you can number the actions/literals to make the constraints
shorter to write)
(b) [4 points] In terms
of n, how many levels in the planning graph will be expanded before
a working plan for the n box problem can be found? No explanation
is required. When you count the number of levels, count both action
and proposition levels. For example, the number of levels in the graph
you expanded in part (a) is 3..
(c) [5 points] In the general
n-box problem, what mutex relations will there be between the propositions
at proposition level S1? No explanation required.
(d) [6 points] Let n >
2. What mutex relations will there be between propositions at proposition
level Sk for k >= 3? Briefly
justify your response.
(e) [5 points] For n >
2 and k > 3, what mutex relations will there be between actions
in an action level Ak
of the planning graph? Briefly justify your response.
(f) [5 points] How many
levels in the planning graph will be expanded before a planning algorithm
first considers it worthwhile to search for a working plan in the
n-box problem? (Use the same way of counting levels as in (b).) Provide
a one-sentence explanation.
2. [11] It is often said informally
that Graphplan will produce step-optimal solutions
(meaning that a literal appears at the earliest time step possible considering
maximum parallel actions), as opposed to length-optimal
solutions (fewest steps in serial execution).Explore if this is actually
the case. Consider the following example:
We have empty init state,
and Goal state is {P,Q}. We just have two actions in the domain
- A1 Prec: none Effects: P,W
- A2 Prec: none Effects: Q,~W
(a) [3 pts] What is the
optimal parallel plan for this problem? (note that W has nothing to
do with the goal--so we really don't care if it is true or false.)
(b)[3 pts] What is the plan
that Graphplan will produce for this problem? Is it optimal?
(c) [5 pts]Is there an obvious
way of changing the action interference definition such that we could
find the optimal parallel plan with Graphplan? Why is the obvious
way of doing it not an easy way to implement?
3. [10] Question 11.14 in
the book.
4.[10] (From D. Kahneman &
A. Tversky (1982) "Evidential Impact of Base Rates" in D.
Kahneman, P. Slovic & A. Tversky (eds) Judgement Under Uncertainty
, Cambridge.)
You are a witness of a night-time hit-and-run accident involving a taxi
in Athens. All taxis in Athens are blue or green. You swear, under oath,
that the taxi was blue. Extensive testing shows that under the dim lighting
conditions, discrimination between blue and green is 75% reliable. Is
it possible to calculate the most likely colour for the taxi? (Hint:
distinguish between the proposition that the taxi blue and the proposition
that it appears blue.) What now, given that 9 out of 10 Athenian taxis
are green?
5. [18] Two astronomers, in
different parts of the world, make measurements M1 and M2 of the true
number of stars N in some small region of the sky using thier two telescopes.
Each telescope can also be out of focus (events F1 and F2 with probability
f.) If a telescope is OUT of focus, then the scientist will undercount
by three or more stars (that means that if the true number of stars
N is less than or equal to 3, then the astronomer will count 0 stars).
- [6] Draw a belief network to represent this information.
- [6] Give a conditional probability table for the belief node M1.
For simplicity, only consider N = 1, 2, or 3 and probabilities that
M1 = 0,1,2 or 3 here.
- [6] Suppose M1 = 1 and M2 = 3. What are the possible true numbers
of stars (possible values of N)?.Hint: you can either reason forward,
trying each possible value of N and seeing if the measurements M1
= 1 and M2 = 3 are possible (this is sort of a mental simulation of
the physical process); or you can enumerate the possible focus states
and work backward the possible values of N for each.
6.[21, 3 each] Consider the Bayesian
network below. The domain of each variable is {true, false}. For convenience,
each variable has a one letter abbreviation. Instead of showing the
conditional probability tables, we have indicated the qualitative nature
of the causal influences in the network. A plus indicates a positive
influence, and a minus indicates a negative influence. If there is a
positive influence from X to Y, then P(y|x) > P(y| ~x), and visa
versa for a negative influence. (Note: P(y| ~x) is shorthand for P(Y=true|X=false),
etc.) This relationship holds for all values of the other parents
of Y.
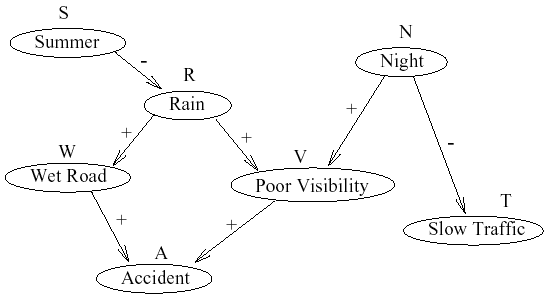
For example, in the given
network we can infer, amongst other things:
- P(t|n) < P(t|~n)
- P(v|n,r) > P(v|n, ~r)
- P(v|~n,r) > P(v|~n, ~r)
You should also assume that "explaining away" occurs whenever
there are two edges labeled + going into a node, e,g,
P(r|v,n) < P(r|v) because the presence of Night "explains
away" the Poor Visibility.
Your goal is to determine, for each of the pairs of conditional probability
values below whether one is larger than the other, they are equal, or
they are incomparable with the information we have given you.
- (a) P(s|v) and P(s)
- (b) P(v|t) and P(v)
- (c) P(s|v,~n) and P(s|v)
- (d) P(w|v) and P(w)
- (e) P(w|a,v) and P(w|a)
- (f) P(w|r,v) and P(w|r)
- (g) P(w|a,r,v) and P(w|a,r)
============
EXTRA CREDIT
============
Imagine that we want to do
planning in a multiagent situation. Since the agents can work at the
same time, actions are allowed to occur in parallel. Assume that we
have an unbounded number of agents, so we can put as many actions in
parallel as we want. Thus, at each phase i, we will now choose not a
single action, but a set of actions Si all of which will take place
in parallel. For any Si, we have no guarantees about which action in
Si will get completed first. We can only guarantee that all actions
in Si get completed within the time phase of the plan, i.e., before
any of the time i + 1 actions are started. In other words, all we know
is that the actions in Si start and end at some point during phase i.
[15 points] Come up with a
good definition of the notion of a parallel plan. In other words, we
want to provide a constraint on the sets Si that guarantees that no
matter how actions are executed within a phase, the result of the execution
is the same. More precisely, let S be a set of actions and let w be
a state in which all of the preconditions of all of the actions in S
hold. State the assumptions on S that guarantee that, no matter the
order in which the actions in S are executed, the result of applying
S in w is the same.
|
|
