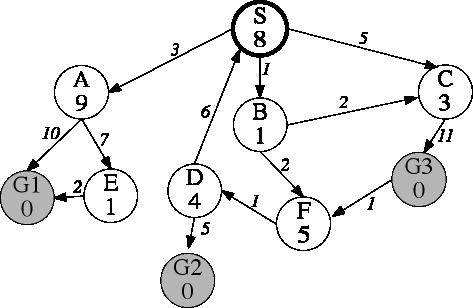
Written Homework #2

Due Mar 6

1. [35] Consider the following state-space graph with Start State S and Goal states G1, G2, and G3, heuristic function values and path costs noted:

Assuming that successor states are generated in alphabetical order (in stack-based algorithms, placed on the Open List in alpha order either at the start or at the end), and ties (for priority-queue based algorithms) broken in alphabetical order, in what order are the nodes in this graph expanded by each of the following search algorithms (tree search)? Also for each, what is the cost of the path found? If the path found is not optimal, briefly explain why the algorithm didn't find the optimal path. Do not remove repeated states.

• Breadth-First Search: I'll do this one for you: expanded=SABCEG1, path (SAG1) cost is 13 (not optimal), the open list still has C(via B) F (via B) G3 (via C) G1(via E) on it.  You still need to tell me *why* it didn't find the optimal answer. Here's how I got this answer: we start by expanding S, which places A B C (in that order) on the open list. Then we expand A, placing E then G1 at the end of the open list, then expand B, placing C and F on the end of the open list, then expand C, placing G3 at the end, then E placing G3 at the end, then expand G1, finishing with S-A-G1.
• Depth First Search
• Uniform Cost Search
• Iterative Deepening
• Greedy Best-First Search
• A*
• IDA*

2. [15] Problem 3.17 from the book. (five parts)

3. [8] Problem 4.2 (four parts)

4. [8] Problem 5.4 (two parts)

UNDERGRADS (481): Only those taking 481 need to do problems 5, 6 and 7.

5. [9] (a) Describe a search space where iterative deepening performs much worse than depth-first search.

          (b) Construct a finite search tree for which it is possible that depth-first search
uses more memory than breadth-first search. (Be sure to show the goal node(s) in your
tree.)

          (c) Is there any tree and distribution of goal nodes for which depth-first search always requires more memory than breadth-first search? Briefly justify your answer.

6. [15]  Problem 4.9 (there are three parts)

7. [10] In the "Four-Queens puzzle", we try to place 4 queens on a 4x4 chess board so that none can capture any other (that is, only one queen can be on any row, column, and diagonal of the array). Suppose we try to solve this problem with the following problem space: The start node is labeled by an empty 4x4 array; the successor function creates new 4x4 arrays containing one additional legal placement of a queen anywhere in the array; the goal predicate is satisfied iff there are four queens in the array (legally positioned).

• Invent an admissible heuristic function for this problem based on the number of queen placements remaining to achieve the goal. (Note that all goal nodes are precisely four steps from the start node!)
• Use your h function in an A* search to a goal node. Draw the search tree consisting of all 4x4 arrays produced by the search and label each array by its value of g and h. (Note that symmetry considerations allow us to generate only three sucessors of the start node).
  

GRADUATES (681): Only those taking 681 need to do problems 8–11.

8. [9] Prove that if a heuristic function h is monotonic (consistent), then it is admissible. Recall that “h is consistent” means
          h(n) ≤ c(n,a,n') + h(n')

where n' is a direct successor of n via action a.

Graduate students taking the prelims are also responsible for the material in Chapter 6 of Russel and Norvig on Game Tree searching. In particular, you'll want to understand minimax and alpha-beta pruning.

9. [16] Problem 6.1 in the book; parts b, c, d, and e.

10. [5] 6.12, part a.

11. [4] The minimax algorithm returns the best move for MAX under the assumption that MIN plays optimally. What happens when MIN plays suboptimally?