How many possible mantissas can be represented in single precision?
Answer:
A mantissa has 23 bits so there are 223
patterns possible.
How many possible mantissas can be represented in single precision?
A mantissa has 23 bits so there are 223
patterns possible.
An IEEE 754 single-precision floating point value is 32 bits long. The bits are divided into fixed-sized fields as follows:
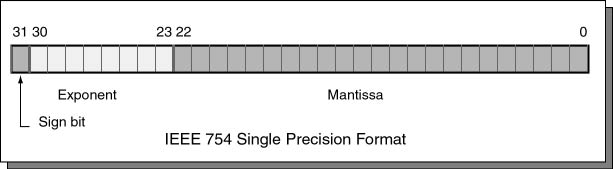
Bits 0 through 22 are for the mantissa; bits 23 through 30 are for the exponent; and bit 31 is the sign bit. The mantissa and exponent fields work like the similar parts in scientific notation (details follow). The sign bit gives the sign of the entire expression: a 0 bit means positive and a 1 bit means negative.
You have seen the MIPS instruction bltz which
branches if the 32-bit integer in a register is less than zero
(negative).
It does this by looking at bit 31 of the two's complement integer
and branching if it is set.
Does this instruction work with single precision values?