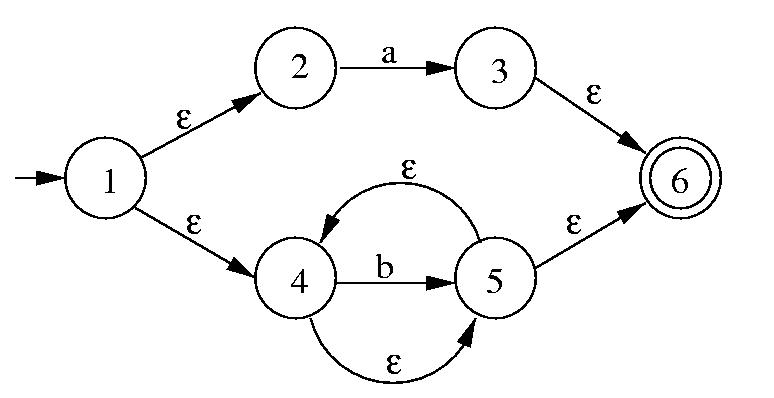
The state table for this is (e = epsilon)
| State | a | b | e |
|---|---|---|---|
| 1 | {} | {} | {2,4} |
| 2 | {3} | {} | {} |
| 3 | {} | {} | {6} |
| 4 | {} | {5} | {5} |
| 5 | {} | {} | {4,6} |
| 6 | {} | {} | {} |
The DFA is constructed from subsets of the NFA states:
| State subsets | a | b |
|---|---|---|
| {1,2,4,5,6} | {3,6} | {5,4,6} |
| {3,6} | {} | {} |
| {4,5,6} | {} | {5,4,6} |
| {} | {} | {} |
Renumbering the states, this table becomes
| State | a | b |
|---|---|---|
| 1 | 2 | 3 |
| 2 | 4 | 4 |
| 3 | 4 | 3 |
| 4 | 4 | 4 |
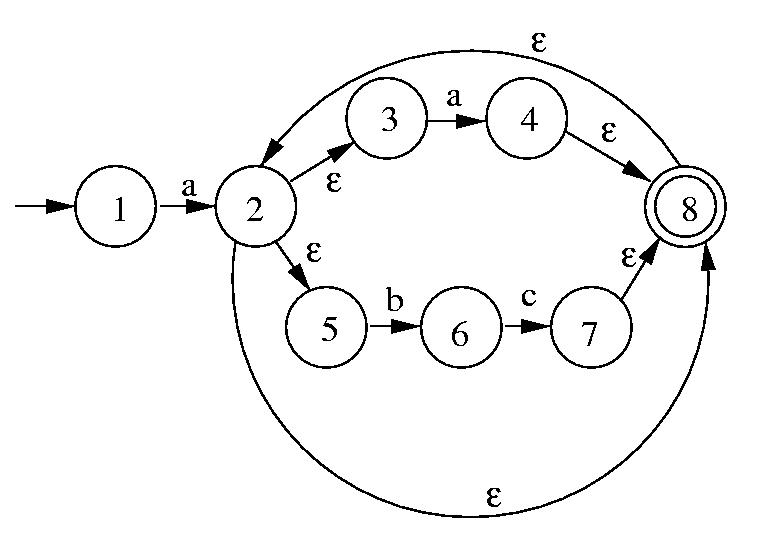
The state table for this is (e = epsilon)
| State | a | b | c | e |
|---|---|---|---|---|
| 1 | {2} | {} | {} | {} |
| 2 | {} | {} | {} | {3,5,8} |
| 3 | {4} | {} | {} | {} |
| 4 | {} | {} | {} | {8} |
| 5 | {} | {6} | {} | {} |
| 6 | {} | {} | {7} | {} |
| 7 | {} | {} | {} | {8} |
| 8 | {} | {} | {} | {2} |
The DFA is constructed from subsets of the NFA states:
| State subsets | a | b | c |
|---|---|---|---|
| {1} | {2,3,5,8} | {} | {} |
| {2,3,5,8} | {4,8,2,3,5} | {6} | {} |
| {} | {} | {} | {} |
| {2,3,4,5,8} | {4,8,2,3,5} | {6} | {} |
| {6} | {} | {} | {7,8,2,3,5} |
| {2,3,5,7,8} | {4,8,2,3,5} | {6} | {} |
Renumbering the states, this table becomes
| State | a | b | c |
|---|---|---|---|
| 1 | 2 | 3 | 3 |
| 2 | 4 | 5 | 3 |
| 3 | 3 | 3 | 3 |
| 4 | 4 | 5 | 3 |
| 5 | 3 | 3 | 6 |
| 6 | 4 | 5 | 3 |
The book uses a slightly more complicated way to represent Kleene closure than I do in the above graphs. That leads to more states in the automata constructed from them. Both ways are acceptable.