Model Solutions to Homework Assignment 2, due Monday, September 11, 2000
1. Problem 2.2 (a), page 62.
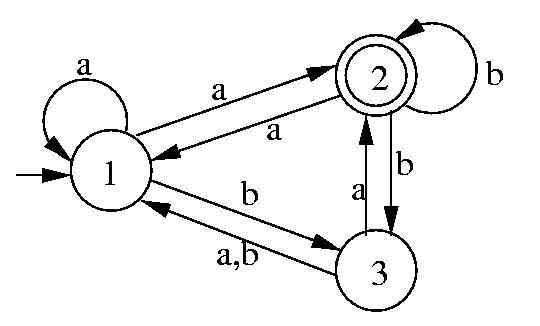
Each string is shown spaced out so that the states of the NFA after reading
each letter can be shown between that letter and the next.
a a a b
1 1 1 1 3
2 2 2 2
aaab is accepted
b a a a b
1 3 1 1 1 3
2 2 2 2
baaab is accepted
a b a b a b
1 1 3 1 3 1 3
2 2 2 2 2 2
ababab is accepted
b a a b b
1 3 1 1 3 1
2 2 2 2
3
baabb is accepted
a b a
1 1 3 1
2 2 2
aba is accepted
Problem 2.2 (b), page 62.
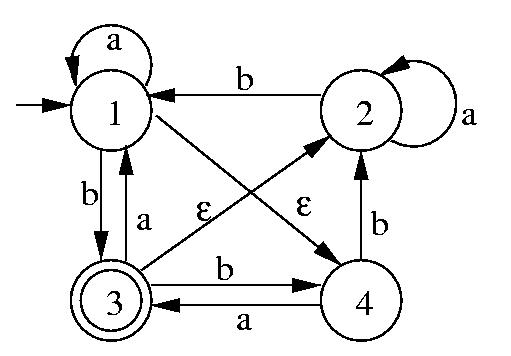
Each string is shown spaced out so that the states of the NFA after reading
each letter can be shown between that letter and the next.
a b a a b
1 1 3 1 1 3
4 3 4 3 2 1
2 1 2 3 4
2 4 4 2
abaab is accepted
b a a b b
1 3 1 1 3 4
4 2 2 2 1 3
4 3 4 2
4 2 1
baabb is accepted
b b a b a
1 3 4 3 4 3
4 2 1 1 3 1
2 1 2
4 2 4
bbaba is accepted
a a b b
1 1 1 3 4
4 3 3 4 2
4 2 1 3
2 4 2 1
aabb is accepted
b a b a b a
1 3 1 3 1 3 1
4 2 2 1 2 1 3
4 2 3 4 2
4 4 2 4
bababa is accepted
a b b b
1 1 3 4 2
4 3 4 2 1
4 2 1 3
2 1 3 4
abbb is accepted
Problem 2.2 (c), page 62.
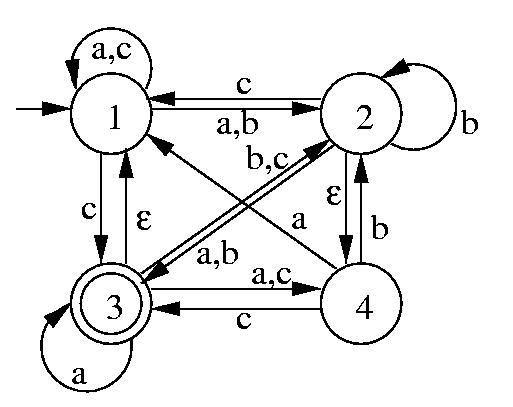
Each string is shown spaced out so that the states of the NFA after reading
each letter can be shown between that letter and the next.
a b a a b c
1 1 2 3 3 2 1
2 3 4 4 3 3
4 4 1 1 4 2
1 2 2 1 4
abaabc is accepted
b a c a b b
1 2 3 2 3 2 2
4 1 4 1 3 3
1 2 4 4
3 4 1 1
bacabb is accepted
c b a b a
1 1 2 3 2 3
3 4 1 4 1
cbaba is accepted
c c a a c c
1 1 1 1 1 1 1
3 3 2 2 3 3
3 3 2 2
4 4 4 4
ccaacc is accepted
b a b c b
1 2 3 2 1 2
4 1 1 3 4
4
babcb is not accepted
2. Construct the equivalent DFA for the NFA in problem 2.2 (a).
First, construct the subsets of the states of the NFA.
|
State subsets
|
a
|
b
|
|
{1}
|
{1,2}
|
{3}
|
|
{1,2}
|
{1,2}
|
{2,3}
|
|
{3}
|
{1,2}
|
{1}
|
|
{2,3}
|
{1,2}
|
{2,3,1}
|
|
{1,2,3}
|
{1,2}
|
{1,2,3}
|
Then number the states.
|
State
|
a
|
b
|
|
1
|
2
|
3
|
|
2
|
2
|
4
|
|
3
|
2
|
1
|
|
4
|
2
|
5
|
|
5
|
2
|
5
|
Construct the equivalent DFA for the NFA in problem 2.2 (b).
First, construct the subsets of the states of the NFA.
|
State subsets
|
a
|
b
|
|
{1,4}
|
{1,3,4,2}
|
{3,2}
|
|
{1,2,3,4}
|
{1,2,3,4}
|
{3,1,4,2}
|
|
{2,3}
|
{1,2,4}
|
{4,1}
|
|
{1,2,4}
|
{1,2,3,4}
|
{3,1,2,4}
|
|
{1,4}
|
{1,3,4,2}
|
{3,2}
|
Then number the states.
|
State
|
a
|
b
|
|
1
|
2
|
3
|
|
2
|
2
|
2
|
|
3
|
4
|
5
|
|
4
|
2
|
2
|
|
5
|
2
|
3
|
Construct the equivalent DFA for the NFA in problem 2.2 (c).
First, construct the subsets of the states of the NFA.
|
State subsets
|
a
|
b
|
c
|
|
{1}
|
{1,2,4}
|
{2,4}
|
{1,3}
|
|
{1,2,4}
|
{1,2,3,4}
|
{1,2,3,4}
|
{1,3}
|
|
{2,4}
|
{1,3}
|
{1,2,3,4}
|
{1,3}
|
|
{1,3}
|
{1,2,3,4}
|
{2,4}
|
{1,2,3,4}
|
|
{1,2,3,4}
|
{1,2,3,4}
|
{1,2,3,4}
|
{1,2,3,4}
|
Then number the states.
|
State
|
a
|
b
|
c
|
|
1
|
2
|
3
|
4
|
|
2
|
5
|
5
|
4
|
|
3
|
4
|
5
|
4
|
|
4
|
5
|
3
|
5
|
|
5
|
5
|
5
|
5
|
3. Problem 2.7, page 63.
Given R = (ab|b)*c,
ababbc is in L(R).
c is in L(R).
babc is in L(R).
abab is not in L(R).
4. Problem 2.8, page 63.
Given R = ab*c(a|b)c,
acac is in L(R).
acbbbc is not in L(R).
abcac is in L(R).
abcc is not in L(R).
5. Problem 2.9, page 63.
One solution is b|b(a|b)*b. This is the same as b|(b(a|b)*b).
Another solution is b|((a|b)*b|e) where e is epsilon.
6. Problem 2.10, page 63.
One solution is ((a|b)(a|b)(a|b))*.


