Lattice Computers
A lattice is essentially a discrete analog of a vector space and is of importance, for example, in crystallography.
In crystallography A3, the face-centered cubic lattice (found, for example, in crystalline argon), is based on a standard, space-efficient stacking of oranges or cannon balls. Below is a picture of a tiny lattice computer where the identical, synchronized processors (pictured as big spheres) are connected (by identical communication links) to A3-lattice nearest neighbors.
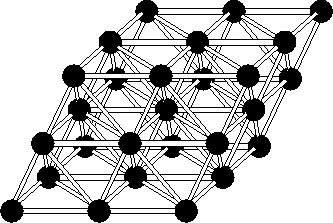
This project has involved developing theoretical underpinning and algorithms for lattice-connected, parallel processing computers, which computers are intended to provide useful, natural, and provably controlled, efficient simulations of the motion of objects in space. The algorithms developed (and being developed) show that controlled, discrete, linear in real time, analog simulation of continuous motion is possible and feasible in lattice computers. Our algorithms to date can found in the REPRESENTATIVE PUBLICATIONS below together with Anil Shende's Ph.D. dissertation, done under my direction:
-
Anil Shende,
Digital Analog Simulation of Uniform Motion in Representations of Physical
N-Space by Lattice-work MIMD Computer Architectures, Ph.D.
Dissertation, Department of Computer Science, SUNY/Buffalo, 1991.
Here, for example, is what our algorithms for simulating continuous motion of a single particle are supposed to do. We work with a picture just below of a small lattice computer based on the lattice A2, the two dimensional version of A3 above.
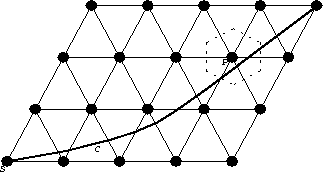
Imagine a particle traveling, in the parallelogram bounded region depicted, along the curve C, moving, say, toward the the upper right hand corner. An algorithm for simulating this motion should, in effect, `light up'' a processor resting on any corresponding lattice point P exactly during the time the particle is as close to P as to any other lattice point. Each ``lit up'' processor computes which nearest neighbors should be lit up next, decides when those neighbors should be told to light up, and tells those neighbors to light up at the correct time. Our algorithms to date come as close as we like to this exact timing. (The dashed line bounded hexagonal region shown in the picture is just the Voronoi cell of P, the set of points in the parallelogram bounded region as close to P as to any other lattice point.)
Just below is an animated gif depicting a particle traveling through a 3-D lattice computer, lighting up processors as it goes.
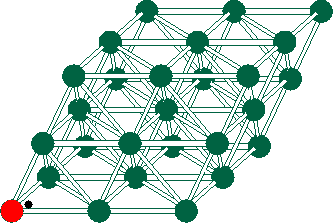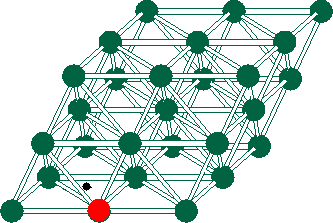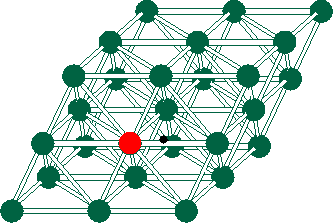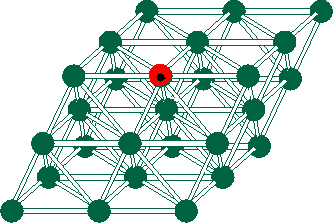
Click just below to see a schematic diagram of a
for the 2-D Lattice A2.Expected eventual applications of this project are to development of intelligent technology for spatial/imagistic reasoning, to real-time control, to scientific computing, and to fundmental understanding of spatial cognition.
In the near future I hope to develop a useful, associated programming environment for lattice computer algorithms, which environment is transportable from one network of workstations to another. Some preliminary (but not updated) thinking on this may be found here.
For an approach different from ours which is further along in developing discrete, analog physics simulations on lattice computers, click here.